Mértani sorozat teljes útmutató: képletek, példák, bizonyítás és alkalmazás a gyakorlatban

Posted byHarrison JonesPosted inUncategorizedTags:, , , , , , , , ,
Mértani sorozat háttérkép
Mértani sorozat teljes útmutató:
képletek, példák, bizonyítás és gyakorlati alkalmazás

📚 Tartalomjegyzék

Mértani sorozat definíciói

A definíciónak többféle megfogalmazása létezik. Mindegyik más szemszögből írja le, hogy viszonyulnak a sorozat tagjai egymáshoz, hogyan kapjuk meg az egyikből a másikat. A sorozat n-edik tagját jelöljük an-el. Például a23 jelöli egy sorozat 23. elemét. Az első elemnél nem mindig írjuk ki alsó indexbe az 1-est.

  • Definíció 1: Azokat a sorozatokat, amelyekben a második tagtól kezdve minden tag az előző tag ugyanannyi szorosa, mértani sorozatnak nevezzük.

    A szorzótényezőt idegen szóval kvóciensnek nevezzük. A leggyakrabban használ jelölései az “r” és a “q”. Ez a deffiníció az alábbi összefüggést írja le a sorozat tagjai között:
    {\Large \boldsymbol{a_{n} \cdot r = a_{n+1} }} , \\[0.5em] {\Large \boldsymbol{ \frac{a_{n+1}}{r} = a_{n}}}
    Például egy olyan mértani sorozat esetén, ahol a szorzótényező 3 (r=3), azaz a sorozat minden tagja az előző tag 3-szorosa, az alábbi áll fenn, ha a kezdőtag 1:
    {\Large \boldsymbol{a _{3} \cdot 3=a_{4}}}, \ \large \text{mivel} \ {\Large \boldsymbol{a_{3}=1 \cdot 3 \cdot 3=9}}, \ \large\text{emiatt} \ {\Large \boldsymbol{9 \cdot 3=27=a_{4}}}
  • Definíció 2: Mértani sorozatnak nevezzük az olyan sorozatokat, amelyekben
    (a másodiktól kezdve) bármelyik tag és az azt megelőző tag hányadosa állandó.

    Ez a hányados ugyanaz, mint az előző deffiníciónál említett szorzótényező, és valójában ez a definíció következik a már ismertetett képlet átrendezéséből:
    {\Large \boldsymbol{\frac{a_{n+1}}{a_{n}} =\ r}}
    Vegyük példának ismételten az r=3 szorzótényezőjű és 1 kezdőtagú sorozatot. Ez a képlet és definíció nem állít mást, minthogy vesszük bármelyik tagot, legyen ez most a 7. tag (729), és az előző tagot, ami a 6. tag (243), akkor ha ezeket elosztom egymással a sorozat szorzótényezőjét, azaz 3-at fogok kapni.
    {\Large \boldsymbol{\frac{a_{7}}{a_{6}} =\ r}},\ {\Large \boldsymbol{\frac{729}{243} =3}}
    De ugye ez is pontosan azt jelenti, hogy minden tag az előző tag 3-szorosa. Lényegében nem csináltunk mást, csak az előző definícióban alkalmazott képletet átrendeztük, és szavakkal leírtuk, hogy így mit jelent.
    • Fontos megjegyezni: A mértani sorozat szorzótényezője – más néven kvóciense – bármilyen valós szám lehet, azaz lehet pozitív, negatív, 0, 1, tört, egész vagy irracionális szám is.
    Ha:
    • „1-nél nagyobb” – ekkor növekvő a sorozat.
    • „1” – ekkor minden tag ugyanaz, sok értelme nincs.
    • „0 és 1 közötti szám” – ekkor csökkenő sorozatról beszélünk.
    • „Negatív egész szám” – a sorozat váltakozó előjelű lesz.
    • „Pozitív vagy negatív tört szám” – csökkenő vagy váltakozó előjelű csökkenő sorozat jellemzi.
    • „Irracionális szám” – matematikailag értelmezett.

    Mértani sorozat n-edik tagjának kiszámítása

    A mértani sorozat egyes elemeit többféleképpen is kiszámíthatjuk, attól függően, hogy melyik ismert taghoz viszonyítunk. Valójában mindegyik módszer ugyanoda vezet, csak más megközelítést alkalmaz — éppen ezért könnyű elveszni közöttük. Érdemes tehát egy helyen összefoglalni a leggyakoribb képleteket, és egyesével, példákon keresztül végigvenni őket.
    Hibalehetőség: A mértani sorozat első tagját nem előzi meg másik tag, ezért az első tag még nem “tartalmazza” a szorzótényezőt! Emiatt van az, hogy az n-edik tagot számolva a szorzótényezőt csak (n − 1) alkalommal kell felhasználni, s szerepeltetni a képletben.

  • Az első taghoz viszonyítva:

    {\Large \boldsymbol{a_{n} =\ a_{1} \cdot r^{n-1}}}

    Ezzel találkozhatunk a leggyakrabban cikkekben vagy tankönyvekben.
    Nem történik más, minthogy az első tagot megszorzom a szorzótényező 1-el kevesebb hatványával, mint ahányadik tagot keresem. Azért az eggyel csökkentett kitevő szerepel, mert az a₁ nem tartalmazza a szorzótényezőt — az csak a második tagtól kezdve jelenik meg.

    Például:
    Sorozat: 1, 2, 4, 8, 16, 32, 64    (r = 2, a₁ = 1)

    {\Large \boldsymbol{a_{6} = a_{1} \cdot r^{6-1} = 1 \cdot 2^{5} = 32}}

  • Az előző taghoz viszonyítva:

    {\Large \boldsymbol{a_{n} =\ r \cdot a_{n-1}}}

    Ennél a módszernél minden egyes tagot az előző tag ismeretében tudunk kiszámítani.
    Egyszerűen csak megszorozzuk az előző tagot a szorzótényezővel r. Ez a módszer különösen jól jön, ha nem ismerjük az első tagot.

    Például:
    Sorozat: 1, 2, 4, 8, 16, 32, 64    (r = 2)

    {\Large \boldsymbol{a_6 = r \cdot a_5 = 2 \cdot 16 = 32}}

  • A következő taghoz viszonyítva:

    {\Large \boldsymbol{a_{n-1} = \frac{a_n}{r}}}

    Ebben az esetben a korábbi tagot számítjuk ki egy ismert későbbi tagból.
    Elég, ha tudjuk a sorozat valamelyik tagját és a szorzótényezőt, és egyszerű osztással visszaléphetünk az előző taghoz. Ez a képlet sem követeli meg tehát az első tag ismeretét. Ez akkor hasznos, ha visszafelé akarjuk rekonstruálni a sorozatot.

    Például:
    Sorozat: 1, 2, 4, 8, 16, 32, 64    (r = 2)

    {\Large \boldsymbol{a_6 = \frac{a_7}{r} = \frac{64}{2} = 32}}

  • Bármely másik taghoz viszonyítva:

    {\Large \boldsymbol{a_n = a_k \cdot r^{n-k}}}

    Ez alapján a képlet alapján bármely ismert tagból kiszámíthatunk egy másikat, természetesen csak akkor, ha ismerjük a szorzótényezőt is.
    A képletben: ak az ismert tag, k az indexe, n pedig a kiszámolandó tag indexe (azaz hogy hányadik tag a sorozatban). Az (n − k) különbség adja meg, hány „lépésnyi” szorzót kell alkalmazni, s ez valójában a két tag “távolsága” lesz a sorozatban.

    Például:
    Sorozat: 1, 2, 4, 8, 16, 32, 64    (r = 2)

    {\Large \boldsymbol{a_6 = a_3 \cdot r^{6-3} = 4 \cdot 2^3 = 4 \cdot 8 = 32}}

    • Egyszerű példák mértani sorozatokra

  • 1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, …
    \Large \textbf{K\'eplet:} \ {\Large \boldsymbol{a_n = 2a_{n-1}}}, \ \large \text{azaz minden tag az el\H{o}z\H{o} tag k\'etszerese} \ {\large \boldsymbol{(r=2,\ a_{1}=1)}}, \\[0.5em] \large \text{Tulajdons\'aga:} \ {\large \boldsymbol{a_n-a_{n-1}=a_{n-1}}},\ \large \text{mivel} \ {\large \boldsymbol{r-1=2-1=1}}
  • 1, 3, 9, 27, 81, 243, 729, 2187, 6561, 19683, …
    \Large \textbf{K\'eplet:} \ {\Large \boldsymbol{a_n = 3a_{n-1}}}, \ \large \text{azaz minden tag az el\H{o}z\H{o} h\'aromszorosa} \ {\large \boldsymbol{(r=3,\ a_1=1)}} \\[0.5em] \large \text{Tulajdons\'aga:} \ {\large \boldsymbol{a_n - a_{n-1} = 2a_{n-1}}},\ \large \text{mivel} \ {\large \boldsymbol{r-1=3-1=2}}
  • 1, 1/2, 1/4, 1/8, 1/16, 1/32, 1/64, 1/128, 1/256, 1/512, 1/1024, …
    \Large \textbf{K\'eplet:} \ {\Large \boldsymbol{a_n = \tfrac{1}{2}a_{n-1}}}, \ \large \text{azaz minden tag az el\H{o}z\H{o} tag fele} \ {\large \boldsymbol{(r=\tfrac{1}{2},\ a_{1}=1)}}, \\[0.5em] \large \text{Tulajdons\'aga:} \ {\large \boldsymbol{a_n - a_{n-1} = -\tfrac{1}{2}a_{n-1}}},\ \large \text{mivel} \ {\large \boldsymbol{r-1 = \tfrac{1}{2} - 1 = -\tfrac{1}{2}}}
    A szorzótényező, mint a példában is, lehet 1-nél kisebb.
  • 5, 15, 45, 135, 405, 1215, 3645, 10.935, 32.805, 98.415, …
    \Large \textbf{K\'eplet:} \ {\Large \boldsymbol{a_n = 3a_{n-1}}}, \ \large \text{azaz minden tag az el\H{o}z\H{o} tag h\'aromszorosa} \ {\large \boldsymbol{(r=3,\ a_{1}=5)}}, \\[0.5em] \large \text{Tulajdons\'aga:} \ {\large \boldsymbol{a_n - a_{n-1} = 2a_{n-1}}},\ \large \text{mivel} \ {\large \boldsymbol{r - 1 = 3 - 1 = 2}} Figyeljük meg, hogy bár az utolsó példában a sorozat kezdőeleme nem 1 volt, hanem az 5, a sorozat képlete és tulajdonsága sem változott a második példához képest. Nyilván nem is változhatott, hiszen ha azt mondom, hogy egy mértani sorozat szorzótényezője 3, akkor az minden körülmények között azt jelenti definíció szerint, hogy a sorozat bármely tagja az előző tag háromszorosa, függetlenül a kezdőértéktől.
  • 1, -3, 9, -27, 81, -243, 729, -2187, 6561, -19683, …
    \Large \textbf{K\'eplet:} \ {\Large \boldsymbol{a_n = -3a_{n-1}}}, \ \large \text{azaz minden tag az el\H{o}z\H{o} tag minusz h\'aromszorosa} \ {\large \boldsymbol{(r=-3,\ a_{1}=1)}}, \\[0.5em] \large \text{Tulajdons\'aga:} \ {\large \boldsymbol{a_n - a_{n-1} = -4a_{n-1}}},\ \large \text{mivel} \ {\large \boldsymbol{r - 1 = -3 - 1 = -4}}
    Negatív szorzótényező esetén a sorozat váltakozó előjelű lesz.
    • 1

    Mértani sorozat összegképlete és bizonyítása

    A mértani sorozat első n tagjának összegét leíró képlet elemzésével és intuitív magyarázatával külön cikkben foglalkoztam, melyet itt találsz. Ha van időd, kérlek olvasd el és véleményezd, mert ezek azok a magyarázatok, amik a blog értelmét adnák.

    A mértani sorozat első n tagjának összegét leíró képletnek több változata is van attól függően, hogy lett rendezve a képlet, ezenfelül a szorzótényezőt rövidíthetik “r” helyett “q”-val is, de mindegyik képlet ekvivalens. Az itt felsorolásra került képletek közül számomra a 3.-nak van nagy jelentősége, pedig az a legkevesebbet használt, mert azalapján érthető meg legkönyebben, miért is működik az összegképlet.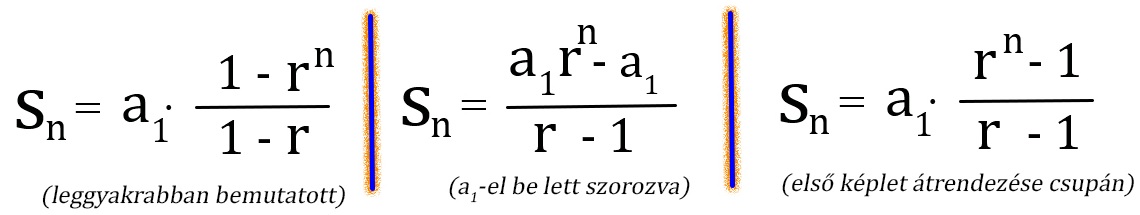

    Ahol: a1→sorozat első tagja, r→szorzótényező, a1rn→ a sorozat n+1-edik tagja, Sn→a tagok összege az n-edik tagig

    Bizonyítás:

    1. lépés:

    A mértani sorozat első n tagjának összegét felírjuk a tagok összegeként, az egyes tagokat pedig a kezdőelem (a1) és a szorzótényező (r) függvényében fejezzük ki:

    {\Large \boldsymbol{S_{n} =\ a_{1} + a_{1} \ \cdotp r^{1} + a_{1} \ \cdotp r^{2} \ + a_{1} \ \cdotp r^{3} \ + a_{1} \ \cdotp r^{4} + a_{1} \ \cdotp r^{5} + a_{1} \ \cdotp r^{n-1}}}

    Az utolsó tag természetesen az n-edik tag lesz. Figyeljünk, hogy mivel az első tag nem “tartalmazza” a szorzótényezőt, ezáltal az n-edik tag eggyel kevesebbszer, n-1-szer fogja “tartalmazni”.

    2. lépés:

    Második lépésként szorozzuk meg az egyenlet mindkét oldalát az “r” szorzótényezővel. Kapjuk, hogy:

    {\Large \boldsymbol{r \cdotp S_{n} =\ a_{1} \ \cdotp r^{1} + a_{1} \ \cdotp r^{2} \ + a_{1} \ \cdotp r^{3} \ + a_{1} \ \cdotp r^{4} + a_{1} \ \cdotp r^{5} + a_{1} \ \cdotp r^{n}}}

    Mi is történt az egyenlet jobb oldalán: Minden egyes tagot egyesével kellett megszorozni az “r” szorzótényezővel. Ez lényegében azt eredményezte, hogy a sorozat tagjai “1-el arrébb csúsztak jobbra”. Minden tag a következő tag lett. Ennek következményeként kiesett az első tag (a1), és az utolsó tag (a1·rn) valójában a sorozat egyel nagyobb tagja lett, mint ameddig kíváncsiak vagyunk a tagok összegére.

    3. lépés:

    Harmadik lépésként összehasonlítjuk a két sorozatot, és elemezzük a kettő közti különbséget, amit lényegében az előző bekezdésben is megtettünk már.

    – Az első lépésben felírt Sn összegképletben van egy extra a1-ünk, amit nem tartalmaz az r·Sn összegképlet.
    – Viszont a második lépésben felírt r·Sn összegképlet tartalmazza a sorozat összeadandó része utáni tagot, amit viszont az Sn nem tartalmazott. (a1·rn).

    Ezt a viszonyt tudjuk az alábbi képlettel kifejezni:

    {\Large \boldsymbol{r \cdotp S_{n} -\ S_{n} =\ a_{1} \ \cdotp r^{n} - a_{1}}}

    4. lépés:

    Negyedik lépésként emeljünk ki a bal oldalon a képletben Sn-t, jobb oldalon pedig a1-et:

    {\Large \boldsymbol{S_{n} \cdotp ( r -1) =\ a_{1} \ \cdotp (r^{n} - 1)}}

    5. lépés:

    Igazándiból meg is kaptuk a képletet, csak rendeznünk kell az egyenletet.
    Osszuk le mindkét oldalt (r-1)-el.

    Kapjuk, hogy:

    {\Large \boldsymbol{S_{n}= a_{1} \cdotp \frac{r^{n} -1}{r-1}}}

    És ezt is akartuk bizonyítani.



    Megjegyzés: Második lépésnél kivonhattuk volna fordítva is: “Sn-r·Sn“, a lényegen nem változtatott volna, csupán a bizonyítás előtt ismertetett 3 féle felírás közül az első kaptuk volna vissza rendezés után.

    Egy bónusz összefüggés

    Ez a rész kicsit kakukktojás, és csak gondolatébresztőnek szánom, hogy milyen sok szempontból is lehet megvizsgálni egy mértani sorozat tagjainak egymáshoz való viszonyát. Hasznos lesz az alábbiak végiggondolása a mértani sor összegképletének megértésekor is. Az összegképlet intuitív magyarázatával külön cikkben foglalkoztam, melyet ide kattinttva érsz el.
    A mértani sorozat első n tagjának összegképlete (a sárgával kiemelt rész miatt fontos az itt bemutatandó tulajdonság):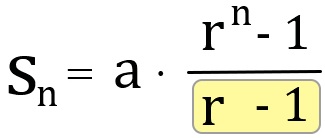

    Ez az alapvető tulajdonság pedig, hogy mértani sorozatoknál bármely tag és az előző tag különbsége az az előző tag r-1-szerese, azaz a szorzótényező 1-el csökkentett többszöröse, vagyis:
    {\Large \boldsymbol{a_{n\ }- a_{n-1}= (r-1) \cdot a_{n-1}}}
    “r-1”, azaz a szorzótényező 1-el csökkentett értéke jelenik meg az első n tag összegét kiszámító képlet hányadosában.
    Nézzünk egy konkrét példát. Vizsgáljuk az r=3 szorzótényezőjű és 1 kezdőtagú sorozat 4. és 5. elemét, mely nem más mint 27 és 81. Az alapvető tulajdonság az alábbi összefüggésre világít rá:
    {\Large \boldsymbol{a_{5}-a_{4}=(r-1) \cdot a_{4}}}, \large \text{vagyis} \ {\Large \boldsymbol{a_{5}-a_{4}=2 a_{4}}}, \ ( \large \text{mivel} \ {\large \boldsymbol{r-1=3-1=2}} )
    {\Large \boldsymbol{a_{5}-a_{4}=81-27= 2 \cdot 27}}, ( \large \text{mivel} \ {\large \boldsymbol{27+2 \cdot 27=81}} )

    Hol alkalmazzuk a mértani sorozatokat a gyakorlatban?

    Pénzügyek-Kamatos kamat

    A pénzügyeinknek szerves részét képezik a mértani sorozatok, de sokszor rá sem jövünk, hogy amikor kamatos kamatról van szó, akár lekötött pénz kamatozásakor, akkor bizony mértani sorozatokat elemzünk. Jól jön tehát a mértani sorozat n-edik tagjának kiszámítására vonatkozó ismeret, amennyiben valaki ki szeretné számolni például, hogy a lekötött pénze fejében mennyit tud majd kivenni a bankból a futamidő végén (az egyszerűség kedvéért most kezelési költséggel és egyéb rejtet költségekkel nem számolunk).
    Tegyük fel, hogy betesz valaki a bankba évi 6%-os kamattal 100.000 forintot 10 évre.
    Először a 6%-ot kell átalakítanunk szorzótényezővé. Hogy a 100.000 forint éves alapon 6%-al gyarapodik, azt így tudjuk felírni:

    1. év végi összeg:
    \large \text{100.000 forint} \cdotp \text{1,06 = 106.000 forint}
    6% kamatnövekmény → 6.000 Ft kamat

    Az első év végére tahát 106.000 forintunk lesz, ami 6000 forint kamatot jelent.
    Következő évben viszont már ez a 106.000 forint fog kamatozni, ez fog növekedni 6%-al. Ezt az alábbiak szerint tudjuk felírni:

    2. év végi összeg:
    \large \text{106.000 forint} \cdotp \text{1,06 = 112.360 forint}
    A kamat összege már 6.360 Ft, mert a kamat is kamatozik.

    112.360 forint van tehát a 2. év végén, ami azt jelenti, hogy ebben az évben már 6360 forint volt a kamat, mert az előző évben keletkezett kamat is kamatozott. Innen ered hát a kifejezés, hogy kamatos kamat.
    A mégtovább növelt összeg kiszámítási képletét át tudjuk alakítani, ha a 106.000 forint helyére behelyettesítjük azt a képletet, ahogy az előző évben kiszámoltuk ezt az összeget.

    Második év képletbe helyettesítve:
    \large (100.000 \cdotp 1,06) \cdotp 1,06 = 112.360
    Már látszik, hogy mértani sor alakja kezd kialakulni.

    És akkor ilyen lépésenként el tudnánk jutni a 10. évig. Az a kérdés, hogy nem tudnánk-e leegyszerűsíteni a képletet valahogy és feleslegessé tenni a minden évben való kiszámolást, ha kizárólag a futamidő végén rendelkezésre álló pénzösszegre vagyunk kíváncsiak? Bizony lehet egyszerűsíteni!

    Általános alak (n-edik év végén):
    {\Large \boldsymbol{a_{n} = 100.000 \cdotp 1{,}06^{n-1}}}
    Mértani sor tulajdonságai: r = 1,06; kezdőtag a1 = 100.000

    Figyelem: Mivel a kezdőtag a 0. évben volt, de a sorozatnak az 1. tagja, így a tizedik év végén levő pénzösszeg valójában a sorozat 11 . tagja lesz!
    Számoljuk hát ki az n-edik tag képlete alapján:

    10 év utáni összeg (valójában a 11. tag):
    {\Large \boldsymbol{a_{11} = 100.000 \cdotp 1{,}06^{10} = 100.000 \cdotp 1{,}79084 = 179.084}}
    Ekkorra a tőke közel megduplázódik.

    A 10. év végén az egyéb költségeket figyelmen kívül hagyva tehát 179.084 forintot vehetek ki a bankból.
    Ez ugyan soknak tűnik, és a kiinduló pénzünkhöz képest az is, sajnos azonban az infláció folyamatosan munkálkodott 10 éven keresztül a háttérben. Bizonyos gazdasági környezetben tehát teljesen valószerű (sajnos a cikk írásának pillanatában is ez a helyzet), hogy ez a pénzzünk kevesebbet ér, mint 10 éve a 100.000 forint.

    Matematika-Fraktálok

    A “fraktál” szó a matematikában használt fogalom, ami egy önmásolódó geometriai mintát vagy alakzatot jelent. A fraktálok olyan struktúrák, amelyek részei vagy önmagukhoz hasonlóak, vagy az egész struktúrától elkülönítve is ugyanolyan mintázatot mutatnak. Gyakorlatilag a fraktálokat sokkal könyebb szemléltetni, semmint definícióval leírni, hogy mik is azok.
    Egy példa a fraktálokra a Koch-görbe. A görbét úgy állíthatjuk elő, hogy egy szabályos háromszög oldalait elharmadoljuk, majd a középső harmadára ismét egy szabályos háromszöget rajzolunk. Az alábbi ábra azt mutatja be, hogyan alakul át a Koch görbe egy újabb iteráció során:

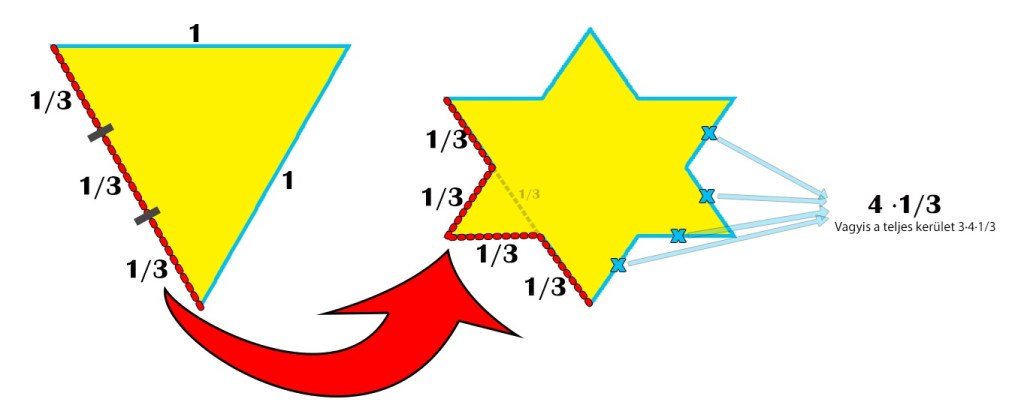
    A Koch-görbe különböző iterációi láthatóak a következő képen:

    A Koch-görbe iterációi. Az utolsó tag ugyanolyannak néz ki, mint az előtte levő, de ez csak azért van, mert olyan változás történik, ami ebben a méretben nem figyelhető meg.
        0. iteráció          1. iteráció          2. iteráció          3. iteráció          4. iteráció      
    3 oldal12 oldal48 oldal192 oldal768 oldal
    33·43·4·43·4·4·43·4·4·4·4

    Az egyes iterációk során kapott oldalak száma, de még a síkidomok kerületének változása is leírható mértani sorozattal.

    Az oldalak számát leíró mértani sorozat:

    A Koch-görbe szerkesztése során az alábbit tesszük:

    • Kiindulásként egy egyenlő oldalú háromszöget használunk, tehát az első iteráció előtt 3 oldal van (ez a 0. iteráció).
    • Minden egyes oldalt felosztunk 3 részre, és a középső harmad helyére két oldal kerül, tehát 1 oldal → 4 oldal.
    • Ezért minden iterációban az oldalak száma négyszereződik.

    Az így kapott mértani sorozat n-edik tagjának kiszámítása:
    {\Large \boldsymbol{a_{n} =\ 4}} \ \cdotp \ {\Large \boldsymbol{a_{n-1}}} \\[0.7em] {\Large \boldsymbol{a_{n} =\ a_{1} \ \cdotp 4^{n-1}}}

    A kerület változását leíró mértani sorozat:

    A kerületeket megadó mértani sorozatot már egy kicsit nehezebb leírni. Gondoljuk végig az alábbiakat:
    1. Az oldalak négyszereződnek minden iterációval.
    2. A kerület nem fog négyszereződni, mert az oldalak kisebbek lesznek.
    3. Mennyivel lesznek kisebbek? Harmadakkorák lesznek minden iterációval.
    4. Tehát, hogyha tudom bármely Koch-görbe kerületét, akkor azt csupán meg kell szoroznom 4-el, majd osztanom 3-al ahhoz, hogy megkapjam a következő Koch-görbe kerületét.
    Nyilván, ha a kezdőtag kerületét tudom, akkor a 4/3-al szorzást annyiszor kell elvégeznem, ahányadik iteráció kerületére kíváncsi vagyok. Vagyis a kezdőtag ismeretében az n+1-edik Koch-görbe kerülete (a kezdőtagom a háromszög, melynek minden oldalát egy egységnek veszem), azaz a kezdősíkidomom kerülete 3 egység:
    {\Large \boldsymbol{K_{n\ }=3 \cdotp \left(\frac{4}{3}\right)^{n-1}}}

    One thought on “Mértani sorozat teljes útmutató: képletek, példák, bizonyítás és alkalmazás a gyakorlatban”

    1. Pingback: Mértani sorozat összegképlete – egyszerű magyarázat és bizonyítás lépésről lépésre – Site Title

    Leave a comment