Mértani sorozat összegképlete – egyszerű magyarázat és bizonyítás lépésről lépésre

Posted byHarrison JonesPosted inUncategorizedTags:, , , , , , , ,
Mértani sorozat háttérkép
Mértani sorozat összegképlete:
egyszerű magyarázat és bizonyítás lépésről lépésre

Tartalomjegyzék

Mértani sorozat első n tagjának összege intuitívan

A mértani sorozat első n tagjának összegét egy bonyolultnak tűnő képlettel kapjuk meg. Hogy hogyan jutunk el magához a formulához, azt rengeteg honlapon fel lehet lelni. Azt azonban, hogy miért működik, már nagyon kevés helyen lehet megtalálni, pedig az ilyen magyarázatok adják a matematika szépségét. Ezek nélkül tényleg csak bonyolult képleteknek és egyenletek sokaságának tűnik az egész, ráadásul sok sikerélményt sem ad ezek bemagolása.
A megértéshez fel kell ismerni, hogy az összegképlet nem állít mást, minthogy amennyiben egy mértani sorozat valahányadik (n-edik) tagjáig vagyunk kíváncsiak a tagok összegére, akkor nem kell mást tennünk, minthogy kiszámítjuk a sorozat következő tagját (az n+1-edik tagot), levonjuk belőle a sorozat első tagját, majd elosztjuk azt a hányados egyel csökkentett értékével.
A legtöbbet az alábbi képletekkel találkozhatunk (a felírások ekvivalensek, csupán máshogy van rendezve az egyenlet):
{\Large \boldsymbol{S_{n}= a_{1} \cdot \left(\frac{1-r^{n}}{1-r}\right)}} \longrightarrow {\Large \boldsymbol{S_{n}= a_{1} \cdot \left(\frac{r^{n} -1}{r-1}\right)}}

Az átalakítást a könnyebb megértés miatt csináltam, mert ebből kiindulva tudjuk megérteni a legkönnyebben a formula működését. Általában 1-nél nagyobb szorzótényezőjű sorozatokat vizsgálunk, mint a bemutatandó példában is, és így a számlálóban és a nevezőben is pozitív szám fog szerepelni. Ne feledjük azonban, hogy a szorzótényező lehet 1-nél kisebb is, mely esetben a számlálóban és nevezőben is negatív értékünk lesz. A képlet azonban működőképes marad, hiszen negatívot osztva negatívval is pozitívat kapunk.
Az egyenlet jobb oldalán végezzük el a szorzást a1-el. Kapjuk, hogy:
{\Large \boldsymbol{S_{n} = \frac{a_{1} \cdot r^{n} - a_{1}}{r - 1}}}

Ez utóbbi formája a képletnek teszi igazán lehetővé, hogy átlássuk, miért is működik a mértani sorozat első n tagja összegének kiszámítására. Először nézzük, hogyan is kell értelmezni a képlet egyes elemeit:

Hogy miért működik a képlet, annak megértéséhez csak végig kell gondolnunk, miből is áll elő egy mértani sorozat n+1-edik tagja.
Ehhez nézzünk egy konkrét példát.

Ki szeretnénk számítani azon mértani sorozat tagjainak az összegét a 4. tagig, amelyikben minden tag az előző tag háromszorosa (r=3), és az első tag az 1. Ennek a mértani sorozat az alábbiak a tagjai:
1,3,9,27,81…
Nézzük tehát, hogyan épül fel a sorozat n+1-edik, azaz 5. tagja:

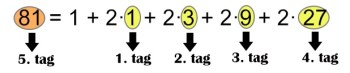
Általánosan elmondható, hogy az r=3 mértani sorozat bármely eleme előáll az első tag plus az előtte levő tagok kétszeresének összegeként. Már ebből jól látható, hogyha az egyenlet bal oldalát leosztjuk 2-vel, akkor visszakapjuk a sorozat első négy tagját, plus 1/2-et.
Hogyhogy pont az első tagot és a további tagok kétszeresét kell összeadni, hogy megkapjuk az n+1-edik tagot?
Kezdjük azzal, hogy ebben a sorozatban hogyan kaptuk meg a 81-et? A sorozat előző tagjának háromszorosa, vagyis 81=3·27. Azonban felírható máshogy is. 81= 27 + 2·27. Ezután a 27-et bontsuk tovább, ami nem más mint 27= 9 + 2·9. És ezt a felbontási folyamatot másoljuk egészen addig, amíg el nem jutnk a sorozat első tagjáig. Az alábbi ábra szemlélteti a folyamatot:

Ugyanezen módon bonthatóak fel a tagok más szorzótényezőjű sorozatoknál is, tehát a magyarázat más mértani/geometriai sorozatoknál is megállja a helyét. Fontos, hogy mindig a kezdő elemet kell levonni az n+1-edik tagból, mert az fog extraként jelentkezni a “felbontás” végén.

Nézzünk egy további példát, ahol a szorzótényező legyen 4, és az első elem pedig nem az 1 lesz, hanem 3. Ennek a mértani sorozatnak az elemei a 6. tagig az alábbiak:
3,12,48,192,768,3072
Amennyiben kíváncsiak vagyunk ezen sorozat első 5 tagjának összegére, akkor kiszámítjuk a sorozat 6. tagját, ami az n+1-edik tag, levonjuk a sorozat kezdőelemét, majd az így kapott összeget osztjuk r-1-el, azaz 4-1=3-al.

Ha tehát az r=4, a=3 mértani sor első 5 tagjának összegére vagyunk kíváncsiak, első lépésként kiszámoljuk az n+1-edik tagot, ami 3072. Levonjuk belőle a sorozat kezdőelemét, ami a 3. 3072-3= 3069. Majd az így kapott értéket elosztjuk a szorzótényező 1-el csökkentett értékével. r-1=4-1=3.
{\Large \boldsymbol{S_{5}= \frac{a_{1} \cdot r^{5} - a_{1}}{r - 1} = \frac{3072 - 3}{4 - 1} = \frac{3069}{3} = 1023}}
Tehát a sorozat első 5 tagjának összege 1023, és az összeadás elvégzésével le is ellenőrizhetjük, hogy tényleg annyi:
3+12+48+192+769=1023

Mértani sorozat összegképletének bizonyítása

A teljesség kedvéért álljon itt a bizonyítás is, de ha szeretnéd az alapokat átismételni, itt találod a mértani sorozatok bevezető cikkét, ami szintén tartalmazza.
A mértani sorozat első n tagjának összegét leíró képletnek több változata is van attól függően, hogy lett rendezve a képlet, ezenfelül a szorzótényezőt rövidíthetik “r” helyett “q”-val is, de mindegyik képlet ekvivalens. Az itt felsorolásra került képletek közül a 3.-at vizsgáltuk a formula működésének megértéséhez az előző fejezetben.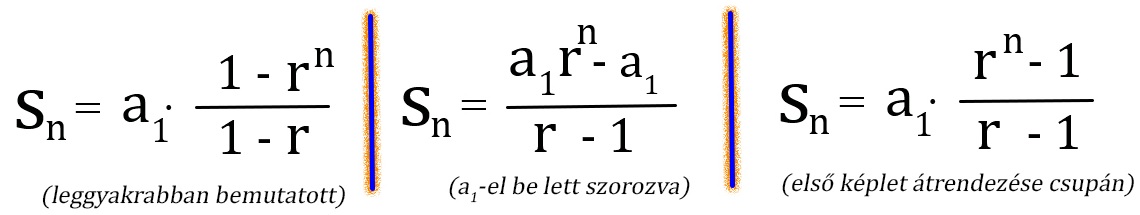

a1→sorozat első tagja
r→szorzótényező
a1·rn→ a sorozat n+1-edik tagja
Sn→a tagok összege az n-edik tagig

Bizonyítás:

1. lépés:

A mértani sorozat első n tagjának összegét felírjuk a tagok összegeként, az egyes tagokat pedig a kezdőelem (a1) és a szorzótényező (r) függvényében fejezzük ki:

{\Large \boldsymbol{S_{n} =\ a_{1} + a_{1} \ \cdotp r^{1} + a_{1} \ \cdotp r^{2} \ + a_{1} \ \cdotp r^{3} \ + a_{1} \ \cdotp r^{4} + a_{1} \ \cdotp r^{5} + a_{1} \ \cdotp r^{n-1}}}

Az utolsó tag természetesen az n-edik tag lesz. Figyeljünk, hogy mivel az első tag nem “tartalmazza” a szorzótényezőt, ezáltal az n-edik tag eggyel kevesebbszer, n-1-szer fogja “tartalmazni”.

2. lépés:

Második lépésként szorozzuk meg az egyenlet mindkét oldalát az “r” szorzótényezővel. Kapjuk, hogy:

{\Large \boldsymbol{r \cdotp S_{n} =\ a_{1} \ \cdotp r^{1} + a_{1} \ \cdotp r^{2} \ + a_{1} \ \cdotp r^{3} \ + a_{1} \ \cdotp r^{4} + a_{1} \ \cdotp r^{5} + a_{1} \ \cdotp r^{n}}}

Mi is történt az egyenlet jobb oldalán: Minden egyes tagot egyesével kellett megszorozni az “r” szorzótényezővel. Ez lényegében azt eredményezte, hogy a sorozat tagjai “1-el arrébb csúsztak jobbra”. Minden tag a következő tag lett. Ennek következményeként kiesett az első tag (a1), és az utolsó tag (a1·rn) valójában a sorozat egyel nagyobb tagja lett, mint ameddig kíváncsiak vagyunk a tagok összegére.

3. lépés:

Harmadik lépésként összehasonlítjuk a két sorozatot, és elemezzük a kettő közti különbséget, amit lényegében az előző bekezdésben is megtettünk már.

– Az első lépésben felírt Sn összegképletben van egy extra a1-ünk, amit nem tartalmaz az r·Sn összegképlet.
– Viszont a második lépésben felírt r·Sn összegképlet tartalmazza a sorozat összeadandó része utáni tagot, amit viszont az Sn nem tartalmazott. (a1·rn).

Ezt a viszonyt tudjuk az alábbi képlettel kifejezni:

{\Large \boldsymbol{r \cdotp S_{n} -\ S_{n} =\ a_{1} \ \cdotp r^{n} - a_{1}}}

4. lépés:

Negyedik lépésként emeljünk ki a bal oldalon a képletben Sn-t, jobb oldalon pedig a1-et:

{\Large \boldsymbol{S_{n} \cdotp ( r -1) =\ a_{1} \ \cdotp (r^{n} - 1)}}

5. lépés:

Igazándiból meg is kaptuk a képletet, csak rendeznünk kell az egyenletet.
Osszuk le mindkét oldalt (r-1)-el.

Kapjuk, hogy:

{\Large \boldsymbol{S_{n}= a_{1} \cdotp \frac{r^{n} -1}{r-1}}}

És ezt is akartuk bizonyítani.



Megjegyzés: Második lépésnél kivonhattuk volna fordítva is: “Sn-r·Sn“, a lényegen nem változtatott volna, csupán a bizonyítás előtt ismertetett 3 féle felírás közül az első kaptuk volna vissza rendezés után.

One thought on “Mértani sorozat összegképlete – egyszerű magyarázat és bizonyítás lépésről lépésre”

  1. Pingback: Mértani sorozat teljes útmutató: képletek, példák, bizonyítás és gyakorlati alkalmazás – Site Title

Leave a comment