Áttérés más alapú logaritmusra intuitívan

A logaritmus azonosságai közül az egyik legnehezebben megérthető az, amelyik leírja, hogyan térünk át más alapú logaritmusra. Lépésról lépésre fogjuk felépíteni az azonosságot, hogy ne csak bemagolás legyen a vége, hanem egy egyszerű analógiával megjegyezhető legyen a képlet.
Alapvetően a logaritmus szavakban kifejezve az alábbit jelenti egy példán keresztül bemutatva:

Ahhoz azonban, hogy ráérezzünk a logaritmus említett összefüggésének képletére, teljesen máshogy kell gondolnunk a logaritmusra. A logaritmus értelmezhető elvontan olyan rendszerként, mint a valuták, csak itt a különböző valutákat nem Forintnak vagy Dollárnak nevezzük, hanem a logaritmus alapja adja meg őket. A logaritmusra tehát gondolhatunk úgy is átvitt értelemben, hogy egy adott szám mennyit ér egy adott rendszerben. Ezt alapul véve megfogalmazható az alábbi:

Ez semmiben nem különbözik attól, mint amikor azt mondom, hogy 400 Forint 2 Eurót ér, csak ez esetben a Forint árfolyama határozza meg az értéket, míg logaritmusnál az alap (példánkban a 3). Nyilván az értékteremtés művelete az (ami alapján azt számoljuk mennyit ér), ami még más lesz:
-Valutáknál az összeadás:
1 Euró +1 Euró= 2 Euró = 400 Ft + 400 Ft = 800 Ft
-Logaritmusnál a szorzás:
2-es alapnál 8=2·2·2=2³ – 3-at ér
2-es alapnál 16=2·2·2·2=2⁴ – 4-et ér

És hogy miért jó így felfogni a logaritmust?
Gondoljuk el azt az esetet, amikor 2 valuta között szeretnék átváltani, azonban nem tudom az egymáshoz viszonyított árfolyamukat, például forintról cseh koronára. Van azonban egy 3. valutám, legyen azaz euró, és ahhoz képest viszont tudom mindkét valuta értékét. Választ tudok-e így kapni arra a kérdésre, hogy 800 Ft az hány cseh koronát ér? A válasz az, hogy igen, és, hogy miért, azt jól szemlélteti az alábbi ábra:

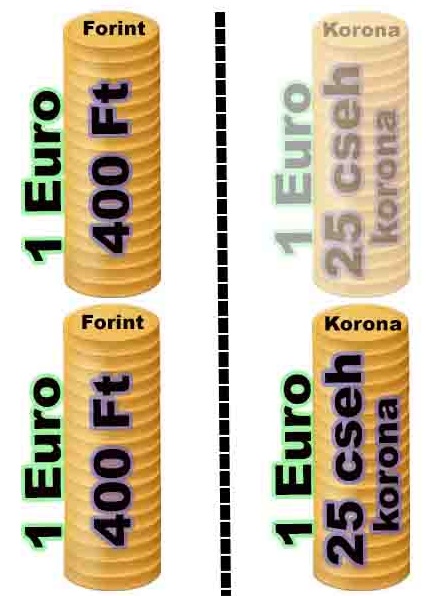
Az ábra könnyen felrajzolható akkor is, ha csak a forint/euró illetve cseh korona/euró árfolyamot tudjuk. Viszont azáltal, hogy tudom mindkét valuta értékét egy harmadik valutához viszonyítva, meg tudom mondani azt is, hogy egymáshoz képest viszonyítva mennyit érnek.
Az ábráról is könnyen leolvasható, hogy 25 cseh korona = 400 forint. A kérdésünk az volt, hogy 800 forint hány cseh koronát ér, a válasz pedig: 800 forint = 2 · 400 forint = 2 · 25 cseh korona = 50 cseh korona.

Amikor áttérünk más alapú logaritmusra, akkor valójában ugyanezt csináljuk, a mögöttes gondolatmenet ugyanez. Van egy számom (előző analógiában ez volt a 800 forint), van egy alapom (előző analógiában ezt volt a cseh korona, valuta), s kíváncsi vagyok, hogy az a szám mennyit ér az alap rendszerében ( előző analógiában 800 forint cseh koronában). Viszont csak azt tudom, hogy egy másik rendszerhez viszonyítva mennyit ér maga a szám és az alap, de ez bőven elég ( a példában a forint és a korona az euróhoz viszonyítva). Az “áttérés más alapú logaritmusra” azonosság a következőképpen írható fel:

Nézzük, hogy hogyan kellene értelmezni az egyes elemeket:

Na de ez a képlet miért analóg a valutátváltás folyamatával? Ennek megértéséhez bevezettem egy log-hoz hasonló jelölést a különböző valutanemek rendszerének jelzésére, de ez valójában tudtommal nem létezik, ne jegyezzétek meg!!! Bevezetése kizárólag szemléltetési célokat szolgál:

Fenti képletbe behelyettesítéssel kapjuk, hogy 1 korona 400/25 azaz 16 forintot ér (természetesen kizárólag 400 forint/euró és 25 cseh korona/euró árfolyammal számolva).

Nézzük meg ugyanezt logaritmusra vonatkozóan egy példán keresztül:

Eredményül tehát az jön ki, hogy a 4-et a másodikonra kell emelni ahhoz, hogy 16-ot kapjunk. Ez tényleg igaz, hiszen 4·4=16.
Fenti példában vizsgáltuk tehát, hogy
– 16 mennyit ér a 2-es szorzási rendszerben (4-et)
– 4 mennyit ér a 2-es szorzási rendszerben (2-őt)
Az jött ki, hogy a dupláját, kétszer annyit ér a 16, ezáltal egymáshoz viszonyítva a 16 pontosan 2-őt ér a 4-es szorzási rendszerben.

Remélem, hogy sikerült fogódzkodót adnom ahhoz, hogy miért is működik ez az összefüggés és miért néz ki úgy, ahogy. Alapvetően a hasonló magyarázatok megosztása a blogom fő célja, nem pedig olyan képletek kimásolása és beillesztése magyarázat nélkül, amelyek más oldalon is megtalálhatóak. Természetesen utóbbi kategóriában is találhatóak cikkek a blogomon, de az csak azért van, hogy egy helyen megtalálja az olvasó a logaritmusra és más témákra vonatkozó anyagokat.

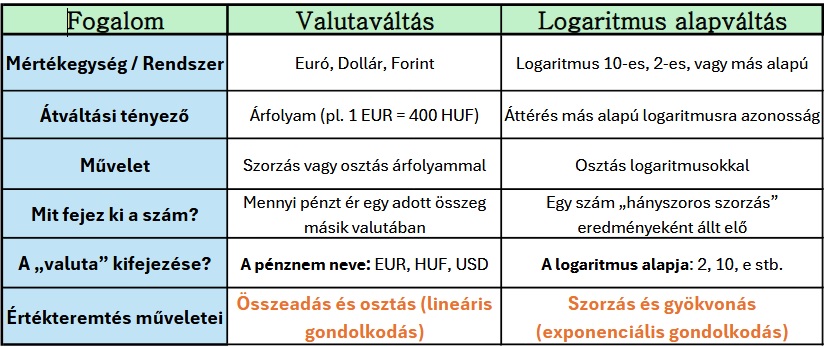
Zárásként pedig egy összehasonlító táblázat a logaritmus és a valuták közti párhuzamok felderítésére: