A logaritmus azonosságai bizonyítással

A logaritmus azonosságai példákkal

A logaritmus azonosságai bevezető
Szorzat logaritmusa: log_a(xy) = log_ax + log_ay
Hányados logaritmusa: log_a(x / y) = log_ax − log_ay
Hatvány logaritmusa: log_a(x^k) = k · log_ax
Áttérés más alapú logaritmusra
Hatvány-logaritmus inverz azonosság
Szorzat logaritmusa intuitívan

Logaritmus azonosságai

Ebben a cikkben az azonosságokat fogom felsorolni, és megpróbálom azokat érthetően elmagyarázni az intuíció fejlesztése végett. A szorzat logaritmusának azonosságát külön fejezetben is megpróbálom hétköznapi példával bemutatni és elmagyarázni, illetve az “áttérés más alapú logaritmusra” azonosságról külön cikk is készült szemléltető ábrákkal.
Az alábbi összefüggésekre/azonosságokra lesz szükségünk a bizonyításoknál (tekintve a logaritmus és hatványozás szoros kapcsolatát célszerű a hatványozás azonosságait feleleveníteni, mielőtt a bizonyítás részek értelmezésébe kezd valaki):

A bizonyításoknál minden esetben új jelölések és képletek bevezetése lesz az első lépés az alábbi alapján:
A logaritmus definíciója szerint minden pozitív valós szám felírható a logaritmus segítségével hatvány alakba következő módon: b = a^log_ab, ahol a, b ∈ℝ⁺, a≠1.
(ℝ⁺ a pozitív valós számok halmazának jelölése, elemei pedig például: 1, 756, 1/2, 16,8 stb…)

A hatványozás azonosságai közül az alábbiakra:
aⁿ · a^m = a^{n + m} Hol: Szorzat logaritmusa
aⁿ / a^m = a^{n – m} Hol: Hányados logaritmusa
(aⁿ)^k = a^{n · k} Hol: Hatvány logaritmusa
+ 1 ráadás: $\Large \boldsymbol{a^{\frac{n}{m}}= \sqrt[m]{a^{n}}}$ (hatvány-logaritmus inverz azonosságnál)

Szorzat logaritmusa

Az azonosság azt mondja ki, hogy szorzat logaritmusa egyenlő a tényezők ugyanazon alapú logaritmusának összegével. Feltételek: a, x, y ∈ℝ⁺, a≠1. Azaz a, x, y pozitív valós számok, a nem lehet 1 (a feltételek szükségessége a definíciónál ismertetve lett).
(ℝ⁺ a pozitív valós számok halmazának jelölése, elemei pedig például: 1, 756, 1/2, 16,8)

Miért működik:

Ahhoz, hogy megértsük miért is működik ez az azonosság, gondoljuk végig a következőt:

Ezek alapján felírható, hogy:

Bizonyítás:

Az “x” és “y” is felírható “a” valahányadik hatványaként. lyenformán két új jelölést bevezetve adódik az alábbi a hatványozás egyik azonosságának felhasználásával:

$\large \text{Ha:} \ {x=a}^{n} \ \large \text{\'es} \ y=a{^{m}} \\[0.5em] \large \text{akkor:} \ \ {\Large \boldsymbol{log_{a} xy=log_{a} a^{n} a^{m} =log_{a} a^{n+m}}}$

Ez azt kérdezi, hogy “a”-t hányadikra kell emelnem, hogy xy-t kapjak, s látható, hogy az “n+m”-edik hatványra. Vagyis:

${\Large \boldsymbol{log_{a} xy=log_{a} a^{n+m} = n+m}}$

Az “n” és az “m” azonban felírható a bevezetett két jelölés alapján logaritmusértékként, melyből nyilvánvalóvá válik az összefüggés:

$\large \text{Mivel:} \ {x=a}^{n}, \ \large \text{ez\'ert:} \ {\Large \boldsymbol{log_{a} x = n}}, \\[0.5em] \large \text{Mivel:} \ {y=a}^{m}, \large \text{ez\'ert:} \ {\Large \boldsymbol{log_{a} y = m}} \ \\[0.5em] \large \text{Behelyettes\'it\'essel ad\'odik, hogy:} \ {\Large \boldsymbol{ log_{a} xy = n + m = log_{a} x + log_{a} y }}$

Hányados logaritmusa

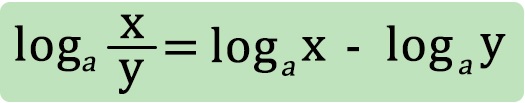
Az azonosság azt mondja ki, hogy egy tört logaritmusa egyenlő a számláló és a nevező ugyanazon alapú logaritmusának különbségével. Feltételek: a, x, y ∈ℝ⁺, a≠1. Azaz a, x, y pozitív valós számok, a nem lehet 1.
(ℝ⁺ a pozitív valós számok halmazának jelölése, elemei pedig például: 1, 756, 1/2, 16,8)

Miért működik:

Ezek alapján felírható, hogy:

Bizonyítás:

A bizonyítás nagyon hasonló az előzőhöz, és az első lépés is ugyanaz, mert ezt is a behelyettesítéses módszerrel tudjuk bizonyítani. Tudjuk, hogy “x” és “y” is felírható “a” valahányadik hatványaként. Ilyenformán két új jelölést bevezetve, s egy hatványozási azonosságot felhasználva adódik az alábbi:

$\Large \text{x=a}^{n} \ \large \text{\'es} \ \Large \text{y=a}^{m} \\[0.5em] {\Large \boldsymbol{log_{a}\frac{x}{y}=log_{a}\frac{a^{n}}{a^{m}}=log_{a} a^{n-m}}}$

Az utolsó sor értelmezése, hogy “a”-t hányadikra kell emelnem, hogy “x/y”-t kapjak, s látható, hogy az “n-m”-edik hatványra. Vagyis:

${\Large \boldsymbol{log_{a}\frac{x}{y}=log_{a}^{n-m}=n-m}}$

Az “n” és az “m” azonban felírható a bevezetett két jelölés alapján logaritmusértékként, melyből nyilvánvalóvá válik az összefüggés:

$\large \text{Mivel:} \ \Large \text{x=a}^{n}, \ \large \text{ez\'ert} \ \ {\Large \boldsymbol{log_{a} x = n}} \\[0.5em] \large \text{Mivel:} \ \Large \text{y=a}^{m}, \ \large \text{ez\'ert} \ \ {\Large \boldsymbol{log_{a} y = m}} \\[0.5em] \ \large \text{Behelyettes\'it\'essel ad\'odik, hogy:} \ \ {\Large \boldsymbol{ log_{a}\frac{x}{y}=n-m=log_{a} x - log_{a} y}}$

Hatvány logaritmusa

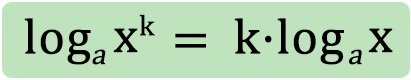
Az azonosság azt mondja ki, hogy egy hatvány logaritmusa egyenlő az alap ugyanezen alapú logaritmusának és a hatványkitevőnek a szorzatával. Természetesen a feltételek itt is érvényesek: a, x ∈ℝ⁺, k∈ℝ, a≠1. Azaz a, x pozitív valós számok, k valós szám, az a pedig nem lehet 1.
(ℝ⁺ a pozitív valós számok halmazának jelölése, elemei pedig például: 1, 756, 1/2, 16,8)

Magyarázatra szorul, hogy a hatványkitevő “k” esetén miért csak annyi van kikötve, hogy valós szám legyen, de pozitívnak a feltételrendszer szerint már nem kell lennie.
A válasz pedig az, hogyha a hatványkitevő negatív is, az x^k akkor is pozitív lesz, hiszen a negatív kitevő azt jelenti, hogy reciprokot kell számolnunk. Negatív “k” esetén is értelmezhető marad tehát az egyenlet.

Hogyan működik:

Az alábbi példában az van bemutatva, hogy mennyit kapok akkor, ha hatványozási azonosságot felhasználva a kitevőt kiviszem a logaritmus elé, továbbá mennyit kapok akkor, ha a logaritmuson belül elvégzem hatványozást. Természetesen ugyanannyi kell, hogy legyen az eredmény:

Bizonyítás:

A logaritmus definíciójából adódik az alábbi azonosság és jelölés:

${\Large \boldsymbol{x= a^{log_{a} x}}}, \ \large \text{melyb\H{o}l behelyettes\'it\'essel ad\'odik, hogy:} \ \ {\Large \boldsymbol{x^{k}= (a^{log_{a} x})^{k}}}$

Ugyanúgy, ahogy az előző két bizonyításnál is tettük, kihasználjuk a hatványozás egyik azonosságát, amiből adódik, hogy:

$\large \text{Mivel} \ {\Large \boldsymbol{a^{x^{y}}=a^{x\cdot y}}}, \large \text{ez\'ert} \ {\Large \boldsymbol{x^{k}= (a^{log_{a} x})^{k}=a^{k\cdot log_{a} x}}}$

Az így kapott összefüggések felhasználásval adódik, hogy:

${\Large \boldsymbol{log_{a} x^{k} =log_{a} a^{k\cdot log_{a} x}}}$

Ez az egyenlet azt írja le, hogy “a”-t hányadikonra kell emelnünk, hogy “a^{k · log_ax}“-et kapjunk. Nyilván pont arra a kitevőre, amire emelve is van a képletben, tehát
“k · log_ax”-re. Mindezeket végiggondolva adódik, hogy:

$\large \text{Mivel} \ {\large \boldsymbol{x^{k}= (a^{log_{a} x})^{k}=a^{k\cdot log_{a} x}}}, \large \text{ez\'ert:} \\[0.5em] {\Large \boldsymbol{log_{a} x^{k} =log_{a} a^{k\cdot log_{a} x}=k\cdot log_{a}x}}$

Áttérés más alapú logaritmusra

A miértekkel részletesen és szemléletesen ezen azonosság esetében külön cikkben foglalkoztam, mivel ez a legnehezebben megérthető azonosság. Kérlek olvasd el azt is, és véleményezd, mert az ott bemutatott magyarázat típusok jelentenék a blogom lényegét.

Ezen azonosság segítségével tudunk egy adott alapú logaritmusról (példában “c”) áttérni egy új logaritmus alapra (példában “a”). A feltételek pedig: a, b, c ∈ℝ⁺, a≠1, c≠1. Azaz a, b, c pozitív valós számok, a és c nem lehet 1 (az alap sosem lehet 1, és most kettő van).
(ℝ⁺ a pozitív valós számok halmazának jelölése, elemei pedig például: 1, 756, 1/2, 16,8)

Bizonyítás:

1. lépés
A logaritmus definíciója szerint minden pozitív valós szám felírható a logaritmus segítségével hatvány alakban az ismertetett jelölésekkel. Azzal kezdjük, hogy az azonosság képletében szereplő két változót felírjuk az alábbi módokon (“c” alapot is felhasználjuk):

Ezekben igazán semmi extra nincs. Nézzük például a 2. képletet, ami nem állít mást, mint hogyha “c”-t arra a számra emelem (log_cb), ami ahhoz kell, hogy “b”-t kapjak, pontosan “b”-t kapok. Mindhárom állítás valójában nyilvánvaló.

2. lépés

Két különböző módon kifejezzük a “b”-t, majd a képletek között egyenlőséget teszünk:

Az 1. és 3. képlet alapján kifejezve:

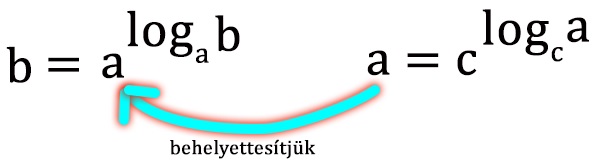
A képlethez tartozó ábra
ezért behelyettesítve:
${\Large \boldsymbol{b=(c^{\log_{c} a})^{\log_{a} b}}}$

A “hatvány hatványa” azonosság felhasználásával kapjuk, hogy:
${\Huge \boldsymbol{b=c^{\log_{c} a \cdot \log_{a} b}}}$

A 2. képlet alapján már az első lépésben kifejeztük:

${\Huge \boldsymbol{b = c^{\log_{c} b}}}$

Mivel mindkettő egyenlet “b” számot fejezi ki, így egyenlőnek kell lenniük.

3. lépés

Egyenlőséget teszünk a két egyenlet között (megtehetjük, hiszen mindkettő “b”-t fejezi ki).

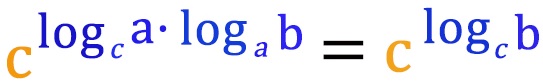
A szám “c” mindkét oldalon megegyezik, ezáltal az egyenlet csak úgy marad egyenlő, ha a hatványkitevők is egyenlőek (fenti képen mivel narancssárga egyenlő, így a kékeknek is annak kell lenniük az egyenlőség teljesüléséhez).

4. lépés

Mivel a hatványkitevők (fenti képen a kékek) egyenlőek, így kapjuk, hogy:

A képlet rendezésével meg is kapjuk az azonosságot (leosztunk “log_ca”-val):

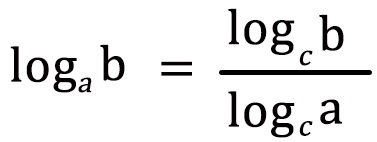
És ezt is akartuk bizonyítani!

Hatvány-logaritmus inverz azonosság

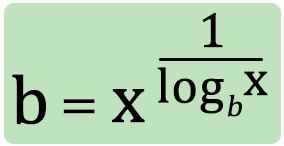
Ez az azonosság nem tartozik a “klasszikus” névvel ellátott azonosságok közé, azonban egy teljesen más irányból mutatja be a logaritmus tulajdonságait, ezért érdemes végiggondolni, hogy miért is működik a fenti képlet. Nevezhetjük még “logaritmus-reciprokos hatványazonosságnak”, angolul pedig leggyakrabban “inverse base identity”-ként hivatkoznak rá.
Igazándiból az azonosság lényegét és hogy miért működik az alábbi kép jól összefoglalja:

Az alábbi magyarázat időben előbb készült, mint a fenti kép, ezért, bár szerintem sok plust a képhez nem ad, és kicsit a túlmagyarázás kategória, nincs szívem törölni (ha mégis ad hozzá plust, és hasznos ez is, akkor egy visszajelzést szívesen fogadok):

1. lépés

Mit fejez ki a log_bx a hatványban?

A logaritmus definíciójából következik, hogy azt a számot, amire “b”-t kell emelnem, hogy “x”-et kapjak, vagyis az alábbit:

Vagyis “b”-t pont arra a számra emelem, ami ahhoz kell, hogy “x”-et kapjak.

Példa:

Legyen b = 2, x = 32. Ekkor:

Így a képlet szerint:

A példában 2-t pont arra a számra emeltük, ami ahhoz kell, hogy 32-t kapjunk, csupán ezt a hatványt logaritmussal fejeztük ki, nem kiírva, hogy “5”.

2. lépés

Mi történik akkor, ha tört van a hatványkitevőben?

Az azt jelzi, hogy gyököt kell vonni. Tehát formulánk valójában az alábbit fejezi ki:

Példa:

Legyen b = 2, x = 32.
Ekkor:
$\Large \boldsymbol{2 = 32^{\frac{1}{\log_{2} 32}} \quad \longrightarrow \quad 2 = \sqrt[\log_{2} 32]{32}}$
Látható, hogy a képlet működik: tört kitevőből gyök lesz, és visszajutunk az eredeti alaphoz.

3. lépés

Lényegében tehát nem történik semmi más, csak két különböző irányból vizsgálom ugyanazt az összefüggést:

Az első képlet “b”-ből építi fel az “x”-et logaritmus segítségével. A második képlet az “x”-ből fejti vissza “b”-t – gyökvonással.

Lényegében ugyanazt az összefüggést járjuk be, csak két különböző irányból.

Példa:

Legyen b = 2, x = 32

A képlet szerint: ha 32-ből olyan gyököt vonok, amekkora a logaritmus, akkor megkapom a 2-őt visszafelé.

Szorzat logaritmusának magyarázata

(baktériumszaporodásos szemléltetéssel)

Ebben a fejezetben megpróbálom bemutatni az említett azonosság magyarázatát képekkel, hátha így könyebb lesz vizualizálni.
A logaritmust gyakran alkalmazzuk olyan természetes folyamatok modellezésére, amelyekben az állapotok egymástól állandó szorzóval térnek el. Jó példa erre a baktériumok osztódása, amikor minden ciklusban megkétszereződnek. Az ilyen növekedés jól leírható a következő képlettel:

Ebben a rendszerben a logaritmust arra tudjuk felhasználni, hogy a darabszám (Sn) és az osztódás gyorsasága (2) ismeretében kiszámoljuk, hogy hány ciklus, azaz osztódás történt, míg a baktériumkolónia elérte a megadott darabszámot.

Vizsgáljunk tehát egy olyan esetet, amikor a baktériumok darabszáma minden ciklusban duplázódik, s a kiinduló baktériumaink száma 1. Azt kérdezzük, hogy hány ciklus alatt nő a baktériumkolónia mérete 8 db-osra?
Mivel minden ciklusban 2x annyi baktériumunk van, így valójában azt kérdezzük, hogy hányadik hatványra kell emelni a 2-őt, hogy 8-at kapjunk. Itt jön a képbe a logaritmus:

Azaz 3 osztódásnak (ciklusnak) kell történnie ahhoz, hogy az 1 db baktériumunkból 8 legyen.
Ezután a baktérium kolóniámat felügyelet nélkül hagyom, majd amikor másnap visszamegyek a laborba, megdöbbenve tapasztalom, hogy 4x annyi baktérium van a kolóniában, mint amikor elmentem. Feltételezve, hogy a sokszorozódás üteme nem módosult, hogyan tudnám kiszámolni, hogy hány duplázódás (ciklus) telt el a kezdetektől?
(Nyilván egy egyszerűen kiszámolható példát választottam, de csak a jobb érthetőség kedvéért. Anélkül próbáljunk meg válaszolni a kérdésre, hogy a tényleges szorzásokat elvégeznénk.)
Itt jön a képbe a szorzat logaritmusa, ugyanis ennek megválaszolásához az alábbi egyenletet kell kiszámítanom:

A kérdés megválaszolásához, és hogy a szorzat logaritmusa miért egyenlő a tagok külön-külön vett logaritmusának összegével, készítettem az alábbi képet:
Külön ki kell tehát számolnom, hogy hány ciklus alatt 4-szereződik meg a baktériumaim darabszáma. Ez nagyon egyszerű:

Tehát 2 ciklus alatt 4-szereződik meg a baktériumaim darabszáma, és ez független attól, hogy hány ciklus telt el (hány baktériumom van). 8, 16 és 32 db baktériumnak is további két ciklusra van szüksége, hogy meg 4-szereződjön a darabszám.
Tehát azt tudtuk, hogy 8 darab baktériumunk 3 ciklus elteltével jött létre.

Azt is tudjuk mostmár, hogy 2 ciklus kell a meg 4-szereződéshez.

Hány ciklus telt el tehát a szaporodás kezdete óta, mire 8·4=32 darab baktériumunk lett? Ehhez kell az azonosság ismerése vagy a képen látottak értelmezése:

Azaz 5 ciklus (osztódás) elteltével lett 1 baktériumból 32 baktériumunk.
Ezt akár le is ellenőrizhetjük, ha az azonosság használata helyett elvégezzük az x·y szorzást: