7-tel való oszthatóság szabálya- Magyarázat, bizonyítás és példák

Miért érdemes megérteni a 7-tel való oszthatóság szabályait?

Valójában az ilyen bonyolultabb szabályok és összefüggések ismertetése miatt jött létre ez a blog. A többi oszthatósági szabály saját kútfőből is viszonylag könnyen megérthető kellő időbefektetéssel, azonban a 7 oszthatósági szabályaira ez már nem feltétlenül igaz. Az bemutatandó szabályok sajnos már nem olyan kézenfekvőek, mint a 2-vel, 3-mal, 5-tel való oszthatósági szabályok. Sajnos magyarázattal nem sok oldal próbálkozik meg, és még a legalaposabbak is csak a levezetést/bizonyítást mutatják be, de azt már nem, hogy miért is működik a szabály.
Bemagolni a szabályokat sok értelme nincs, hiszen a mindennapi életben sosem lesznek alkalmazva. Akik pedig magasabb szinten szeretnének foglalkozni a matematikával, azoknak is elsődlegesen a mögöttes logika a lényeges, nem maga a szabály.
Kettő szabály is bemutatásra fog kerülni. Aki megérti őket, az meg fogja érteni többek között a 11-el és 13-mal való oszthatósági szabályt is, mert az első szabályban kifejtendő logika mentén működnek. Ez az oka annak, hogy viszonylag hosszan lesz taglalva, mert ha valaki ezt megérti, az megért vele még egy csomó más oszthatósági szabályt is.
Megköszönöm, ha hagysz egy kommentet, hogy mennyire segítettek az alább bemutatandó magyarázatok és vizualizációk, ugyanis célom nem egy sokadik blog létrehozása, mely csak egyszerűen felsorolja a szabályokat, hanem a miértek megértéséhez is adjon némi segítséget és motivációt.

7-tel való oszthatóság szabályai és magyarázatuk

Szabály 1-A kétszeres kivonásos módszer

7-tel való oszthatóság alapszabálya: Akkor osztható egy szám 7-tel, ha az utolsó szám előtti számjegyekből képzett számból kivonom az utolsó szám kétszeresét, és az így kapott szám osztható 7-tel.

A módszer magyarázata

A szabály megértése két dolog felismerésén alapszik:
–A 21 osztható 7-tel, azaz 20-hoz még 1 kellene, hogy osztható legyen vele.
–Egy szám kétszeresét könnyebb vizsgálni 7-tel való oszthatóság szempontjából, mint magát a számot (mert a 10-eseket lehet párosítani 20-asokká, így könyebben vizsgálható, mennyire lenne szükségünk még, hogy számunk biztosan osztható legyen 7-tel).

Egy szám 7-tel történő oszthatóságát szeretnénk vizsgálni. Haladjunk lépésről lépésre:

1. Szorozzuk meg a számot első lépésben 2-vel.

   Megtehetjük, mert az oszthatósági tulajdonság öröklődik:

   – Ha egy szám osztható egy másikkal, akkor a sokszorosa is osztható lesz vele. Ez az esetben tehát oszthatósága nem fog tehát változni, és ez valójában bármely számra igaz.
   – Ha azonban nem volt osztható vele, akkor a 7-tel való osztásra igaz, hogy a szám duplája sem lesz az. Ennek oka, hogyha nem osztható vele, akkor van maradék osztásnál. Nincs azonban olyan maradék összeg 1-6 között (7-tel nem osztható szám leosztása ilyen maradékokat képezhet), amit ha duplázok, akkor 7-tel osztható számot kapok.
   Célunk a lépéssel:
   Egy szám kétszeresének a 7-tel való oszthatóságát könnyebb vizsgálni, mint magának a számnak. Ez elsőre paradoxonnak tűnik, de remélem a cikk végére teljesen világos lesz.
   Miért is könnyebb:
   Mert egy szám kétszeresében minden 10-esünk duplázódik, azaz 20-asokat képeznek, és ezáltal tört érték nélkül számolható, hogy mennyi kellene a számunkhoz, hogy osztható legyen 7-tel (mert 20-hoz 1 kellene, hogy 21 legyen).
   Alábbi ábra szemlélteti, mi is történik pontosan, amikor egy számot megkétszerezünk (11 db 10-esünk van a 114-ben, melyet nem tudnánk párosítani):

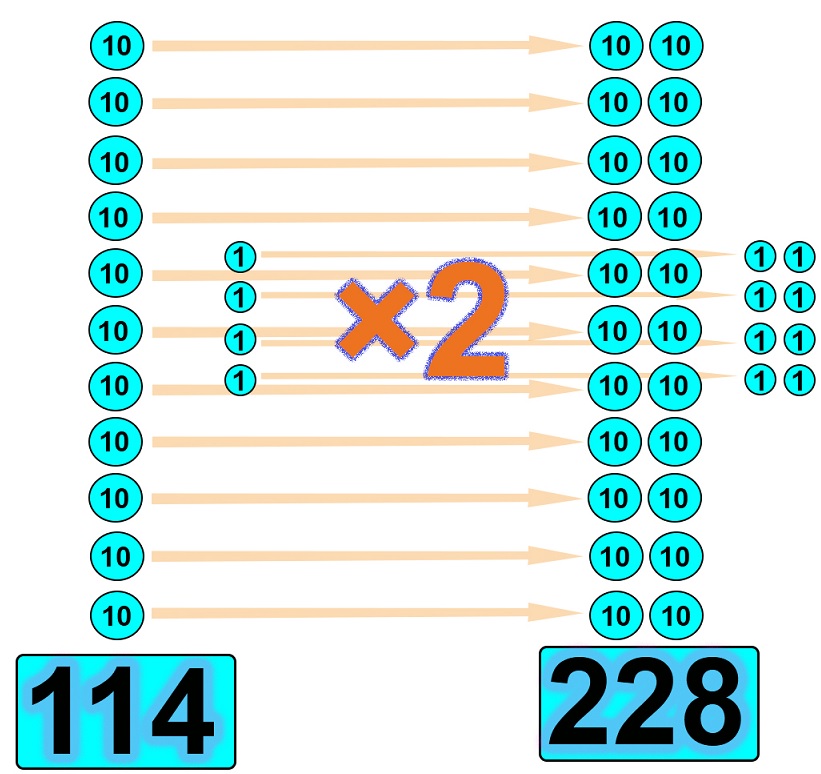
A következő ábra pedig egy konkrét szám esetén mutatja be, hogy hogyan is kell elképzelni, hogy egy szám “20-asait” kiegészítjük 21-re.

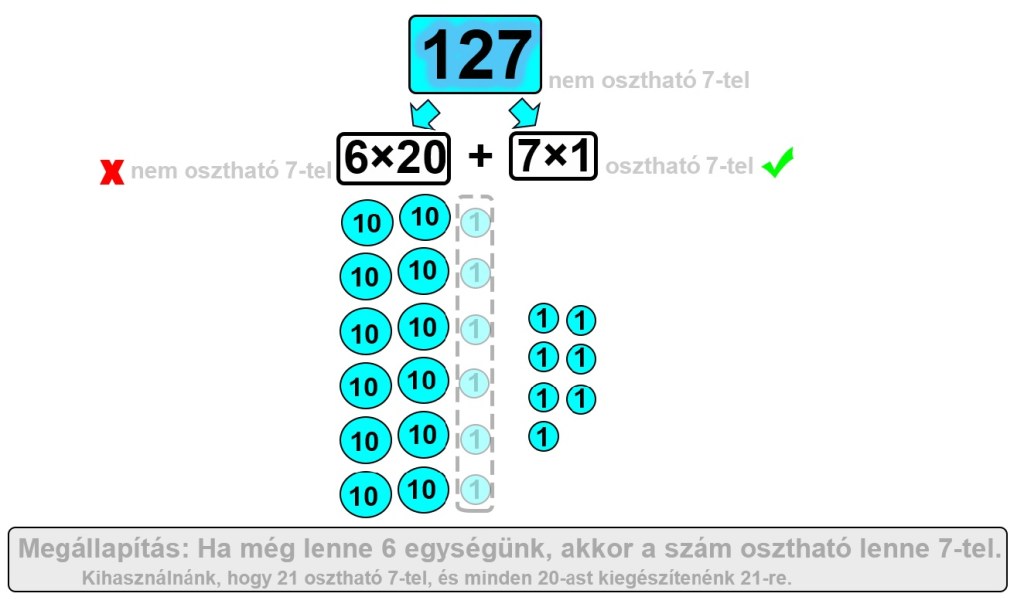
Amennyiben olyan számunk van azonban, amely páratlan sokszor tartalmazza a 10-et (értsd: az utolsó számjegy előtti számokból képzett szám páratlan), akkor már nem olyan egyszerű hozzárendelni, hogy mennyivel kellene kiegészíteni a számunkat, hogy osztható legyen 7-tel.
Ott van például maga a 10, melyhez ha hozzáadunk 0,5-et (nyilván ha 20-hoz 1 kell, akkor ezen logika mentén a feléhez fele annyi kellene), bizony nem kapunk 7-tel osztható számot, nem is beszélve arról, hogy valójában sokkal többet, 4-et kellene hozzáadni a 10-hez, hogy osztható legyen.
Ha a 10-eseket tudjuk párosítani, akkor viszont nincs ilyen problémánk, ezért kell tehát duplázni a számot, hogy biztosan párosíthassuk őket.

2. Hiány kiszámítása és értelmezése

   Megállapítás:
   Ha egy szám kétszeresének a 7-tel való oszthatóságát vizsgáljuk, akkor tehát könnyebb dolgunk van, mintha magát a számot vizsgálnánk. Ennek oka, hogy tudjuk párosítani a 10-eseket 20-asokká.
   10-esek párosítása példával:
   Ha a számot dupláztuk, akkor hány darab 10-es párunk lesz? Természetesen annyi, ahány 10-esünk volt az eredeti számban. Ez az alábbit jelenti:
   Ha kezdeti számunk A=130, akkor 2A=260. A 260-ban 13-db 20-ast tudunk képezni. Tudjuk, ha minden ilyen 20-ast kiegészítenénk 21-re, akkor biztosan 7-tel osztható számot kapnánk.
   Tegyük is meg, azaz 2A+hiány=260+13=273.
   A 273-ról minden vizsgálódás nélkül megmondható innentől, hogy osztható 7-tel.
   A hiány értelmezése:
   Az első fontos értékünk, amit számításba kell venni, hogy mennyit kellene hozzáadnunk a számunkhoz, hogy biztosan 7-tel osztható számot kapjunk (az egyes helyiértéken álló számokat most még hagyjuk figyelmen kívül). Nevezzük ezt hiánynak.
   Példánkban a hiány 13 volt.
   
   A korábban már látott ábra azt szemlélteti, hogyha a 127-hez hozzáadnánk 6-ot, akkor 7-tel osztható számot kapnánk. Itt a hiány tehát 6 volt.

3. Maradék kiszámítása és értelmezése
   És mi legyen a sorsa az egyes helyiértéken álló számnak?
   Eredeti számunkhoz képest kétszer annyi lesz belőle, mivel dupláztunk. Ezekkel maradékként számolunk, hiszen ezek “rendelkezésre állnak” a számunkba. Innentől kezdve nagyon egyszerű a dolgunk, és kimondható:
   Egy számunk akkor osztható 7-tel, ha a hiány és maradék előjeles összegének abszolút értéke 7-tel osztható számot vagy 0-át eredményez (ne feledjük, a hiány negatív, a maradék pozitív előjellel kerül beszámításra).
   Fontos: Azért beszélünk abszolút értékről, mert nagyobb számok esetén a negatív előjelű hiány jóval nagyobb lesz, mint az egyes helyiértéken álló számnak a kétszerese, azaz a maradék, ezáltal az összegük negatív számot eredményez!
   
   Például 58 esetén így néz ki a gondolatmenet:
   – Szorozzuk 2-vel, 2×58=116
   – A hiány=-5, maradék=2×8=16
   – (-hiány)+maradék = -5+16 =11
   – A 11 nem osztható 7-tel, tehát maga az eredeti számunk, az 58 sem.
   

Tehát a 228 bár nem osztható 7-tel, de ha hozzáadnánk 3-at, akkor az lenne. Ha a másik irányban gondolkodunk, akkor ha elveszek belőle 4-et, akkor is 7-tel osztható számot kapnánk. Hogy szokjuk a jelöléseket, az alábbi két állítás igaz így:
231 ≡ 0 (mod 7)
224 ≡ 0 (mod 7)
A szabályból következik továbbá, hogyha találunk egy páros 13-nál nagyobb számot, ami osztható 7-tel, akkor a fele is az lesz. Azaz, ha 224 osztható 7-tel, márpedig az, akkor 112 is az lesz.
112 ≡ 0 (mod 7)

A módszer bizonyítása

1. Induljunk ki abból, hogy minden természetes szám (jelölje most C) felírható az alábbi alakban:
   
   
   
2. Szorozzuk meg kettővel a számunkat. Azt kapjuk, hogy:
   
   
   Ez a művelet nem változtat a 7-tel való oszthatóságán a számnak, mivel:
   – amennyiben a kiindulási számunk osztható volt 7-tel, akkor a kétszerese is az lesz, mivel annak a többszöröse.
   – ha nem volt osztható, akkor a kétszerese sem lesz az, mivel a 7-tel való osztás után nem kaphatunk olyan maradékot (1 és 6 közötti szám), melynek a kétszerese osztható lenne 7-tel (a kétszerese 2,4,6,8,10,12, melyek közül egyik sem osztható 7-tel).
   
   Ugyanez szakszerűen leírva:
   
   -Amennyiben a számunk osztható 7-tel:
   
   
   -Amennyiben a számunk nem osztható 7-tel:
   
   7-tel való osztás esetén értelemszerűen a maradék 1-től 6-ig terjedhet, ha a számunk nem osztható 7-tel, azaz:
   
   Viszont ezen elemek duplájára is igaz, hogy nem oszthatóak 7-tel, azaz:
   
   Ezzel megmutattuk, hogyha egy szám nem osztható 7-tel, akkor a duplája sem lesz az, tehát nyugodtan meg lehet szorozni az eredeti számunkat 2-vel, nem fog változtatni az oszthatóságon.
   
   
3. Kihasználjuk azt a jelenséget, hogy a 21 osztható 7-tel. Nézzük az alábbi képleteket:
   
   Azt, hogy a 20-hoz még 1 kellene, hogy osztható legyen 7-tel, továbbá ezáltal a 20A-hoz A, az alábbi módon jelöljük:
   
   
   
4. Felismerve, hogy 20A-hoz még A kellene, hogy 7-tel osztható számunk legyen, felírható, hogy a számunk akkor és csakis akkor osztható 7-tel, ha:
   

A módszer logikájának a következménye

Tehát a fő momentum a megértésben annak felismerése volt, hogy valójában a szám kétszeresének a 7-tel való oszthatóságát vizsgáljuk. Remélem sokakban felmerült pár gondolat ennek kapcsán, hogy akkor miért ne lehetne visszafelé alkalmazni ezt a szabályt?
Tehát a szabály alapján “A” 7-tel oszthatóságánál valójában “2A” oszthatóságát vizsgálom.
Na de mi van, ha maga “A” is páros, tehát valaminek a kétszerese, azaz “2B”=“A”, vagyis amikor “B” oszthatóságát vizsgálnám, akkor valójában a dupláját elemezném a szabály szerint, ami meg “A”. Na most akkor hogy is van ez? Ha “A” 7-tel vett oszthatóságára vagyok kíváncsi, akkor “2A”-t vizsgálok, ha meg “B”-ét, akkor “A” oszthatóságát?
Hát ennek így nem sok értelme van. Látszólag.

Valójában pedig van. A kulcs az, hogy az oszthatósági szabályoknál univerzális szabályt keresünk, ami minden számra megállja a helyét.
Nyilván a visszafelé alkalmazás, azaz a 2-vel osztás egyrészről nem alkalmazható páratlan számokra, másrészről páros számok esetén is belefuthatunk következő lépésben páratlan számba (páros számnak a fele lehet páratlan, pl: 226/3=113). Ez egyben sajnos azt is jelentené, hogy sok szám esetén hamar falba ütköznénk.
Olyan szabályokra van szükségünk tehát, amelyek a végtelenségig ismételhetőek, azaz addig, amíg olyan számot nem kapunk, amiről ránézésre el tudjuk dönteni, hogy osztható-e 7-tel vagy sem, és a szabály minden körülmények között megállja a helyét.

Érdemes azonban észben tartani, hogy a 7-tel való oszthatóság öröklődik 2-vel történő szorzáskor és osztáskor is (természetesen csak akkor, ha az osztás eredménye továbbra is egész szám). Ez azt jelenti, hogyha egy páros számunk osztható 7-tel, akkor a kétszerese és a fele is az lesz. Nézzünk egy példát, ahol felezgetéssel el is tudjuk dönteni a 7-tel való oszthatóságot:
896/2 ⇒ 448/2 ⇒ 224/2 ⇒ 112/2 ⇒ 56/2 ⇒ 28/2 ⇒ 14
A 14-ről már könnyű eldönteni, hogy osztható-e 7-tel. Nyilván az, úgyhogy a 896 is osztható 7-tel, meg az összes többi köztes szám is.
Tehát ha látjuk, hogy páros a számunk, és a felezéssel olyan számot kapunk, amiről biztosan tudjuk, hogy osztható avagy sem 7-tel, akkor nem érdemes az ismertetett szabályt alkalmazni, mert akkor a szám fele megadja a választ, hogy eredeti számunk osztható-e 7-tel.

Szabály 2-Csoportosítás hármasával hátulról

7-tel való oszthatóság szabálya: Annak eldöntéséhez, hogy egy természetes szám osztható-e 7-tel, alkossunk a számjegyekből hátulról haladva váltakozva 1-es és 2-es jelölésű csoportokat. Ezt követően adjuk össze az 1-es és 2-es csoportok tagjait külön-külön, majd vonjuk ki őket egymásból. Ha az így kapott szám osztható 7-tel, akkor az eredeti szám is.

Ezt folyamatot mutatja be részletesen az alábbi ábra:


718 nem osztható 7-tel.
Könnyű dolgunk volt, hiszen a 700-ról könnyű eldönteni, hogy az, így meghatározni a következő pár 7-tel osztható számot nem nehéz: 707, 714, 721.

Magyarázat

Itt is a hiányt és a maradékokat vesszük figyelembe. A váltakozó előjel fogja jelezni, hogy hiányként vagy maradékként kerül beszámításra a számhármas.
Azért tudjuk ezt megtenni, mert a 1001 osztható 7-tel. Ez például azt jelenti, hogyha van egy 6 jegyű számom, például a 285.000, akkor kapásból meg tudom mondani, hogyha a számhoz hozzáadok 285-öt, akkor biztosan 7-tel osztható számot kapok (mert a 285 db 1000-es generált egyenként 1 db hiányt). Ezáltal az ezresek helyén álló számhármast hiányként (-) fogjuk kezelni.
Az 1.000.001 már nem osztható 7-tel, így a milliós helyiértékeken levő számhármast maradékként (+) számítjuk be.
Az 1.000.000.001 ismételten osztható 7-tel, azaz tekinthetünk a milliárdok helyén álló számhármasra úgy, mint amik hiányt generálnak.
Az oszthatóság eme mintázat mentén ismétlődik a végtelenségig. Az alábbi ismétlődést használjuk tehát ki:
1 ≡ 1 (mod 7) (maradék)
1.001 ≡ 0 (mod 7) (hiány)
1.000.000 ≡ 1 (mod 7), mert 999.999 osztható 7-tel. (maradék)
1.000.000.001 ≡ 0 (mod 7) (hiány)
1.000.000.000.000 ≡ 1 (mod 7), mert 999.999.999.999 osztható 7-tel. (maradék)
stb…

Gyakorlati haszna ennek az eljárásnak nem sok van, mert hosszadalmas a számolás, viszont új megközelítésbe helyezi az oszthatósági szabályokat, így érdemes végiggondolni és megérteni, hogy miért is működik ez a szabály.

Példák a 7-tel való oszthatóság eldöntésére

• 256
  Szorozzuk meg 2-vel. 256×2=512
  Hiány: 25, Maradék: 6×2=12.
  A hiány és a maradék előjeles összege: (-25)+12=13
  A 13 nem osztható 7-tel, tehát az eredeti számunk, a 256 sem.
• 352.352.168.168
  A szám alakja miatt kapásból megmondható a második szabályt alkalmazva, hogy osztható lesz 7-tel. 2 db 168 számhármasunk van egymás mellett. Az egyik hiány (-) lesz míg a másik maradék (+).
  2 db 352 számhármasunk van egymás mellett. Az egyik hiány (-) lesz míg a másik maradék (+).
  Tehát a hiányok és maradékok kioltják egymást, a számhármasok előjeles összege 0 lesz, vagyis a számunk osztható 7-tel.
• 517.483
  – Szorozzuk meg 2-vel.
  517.483×2=1.034.966
  Hiány : Az utolsó számjegy előtti számokból képzett szám negatívan beszámítva = -103.496
  Maradék: Az utolsó számjegy duplája, azaz 2×6=12
  Hiány+Maradék = -103.496+12 = 103.484
  – Ez a szám még túl nagy ahhoz, hogy eldönthessük ránézésre, hogy osztható-e 7-tel.
  Semmi gond, mert a szabály univerzális, és akárhányszor lehet alkalmazni.
  103.484×2 = 206.968, hiány = 20.686 maradék = 2×8=16
  Hiány+Maradék=-20.686+16=20.670
  – Ez még mindig túl nagy.
  20.670×2=41.340, hiány=4134 maradék=0
  Hiány+Maradék=-4134+0=4134
  – Közeledünk.
  4134×2=8268, hiány = 826 maradék = 2×8 = 16
  Hiány+Maradék= -826+16 = 810
  – 700 osztható 7-tel, tehát elég csak a különbséget vizsgálni.
  810-700=110
  Tudjuk hogy a 70 és a 35 is osztható, tehát az összegük, 105 is.
  Mivel a 105 és a 110 között nem 7 a különbség, így már megállapítható, hogy 810 nem osztható 7-tel, és ebből következőleg az eredeti számunk sem.